|
|
|
|
|
|
|
Ένα σώμα Σ1 με μάζα m1 = 0,1 kg, εκτελεί ταλάντωση σε λείο οριζόντιο επίπεδο, δεμένο σε οριζόντιο ελατήριο σταθεράς k, το άλλο άκρο του οποίου είναι δεμένο σε ακλόνητο σημείο. Η εξίσωση της ταχύτητας του είναι της μορφής υ1 = 10συν10πt (SI). Κάποια στιγμή στη διάρκεια της ταλάντωσής του και καθώς έχει διανύσει το 80% του πλάτους του κινούμενο προς τα δεξιά (κατεύθυνση που θεωρούμε θετική), συγκρούεται κεντρικά και ελαστικά με αντιθέτως κινούμενο σώμα Σ2 μάζας m2. Η κρούση έχει ως αποτέλεσμα το Σ1 να μεταφέρει όλη την κινητική του ενέργεια στο Σ2. Το ποσοστό αύξησης της κινητικής ενέργειας του Σ2 είναι 1500%. Μετά την κρούση τα δύο σώματα ξανασυγκρούονται, στη θέση ισορροπίας του Σ1 (όταν το Σ1 περνά από κει για 2η φο
...
Διαβάστε περισσότερα
|
|
Δύο απολύτως λείες και ελαστικές σφαίρες (ίδιου όγκου διαφορετικής μάζας) είναι τοποθετημένες στο τραπέζι ενός μπιλιάρδου (του οποίου η κάτοψη φαίνεται στο διπλανό σχήμα). Οι κρούσεις με τις σπόντες είναι και αυτές ελαστικές. Τοποθετούμε τη σφαίρα Σ2 σε σημείο που βρίσκεται σχεδόν πάνω στη μεσοκάθετο της μικρής πλευράς. Σχεδόν από την ίδια ευθεία αλλά εκατέρωθεν αυτής εκτοξεύουμε την Σ1 με ταχύτητα έτσι ώστε να συγκρουστεί μη κεντρικά και ελαστικά με την Σ2. Μετά την κρούση, οι δύο σφαίρες αφού ανακλαστούν στις σπόντες περνάνε σχεδόν από το ίδιο σημείο (το θεωρούμε ίδιο) της μεσοκαθέτου (σε διαφορετικές στιγμές όμως). Η μεταβολή της ορμής της Σ1 στην σπόντα έχει μέτρο , όπου το μέτρο της ορμής της Σ1 μετά την κρούση με τη Σ2. Να βρείτε: |
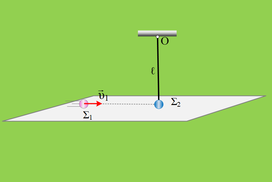
Σφαίρα Σ1 μάζας m1 = 1 kg έχοντας ταχύτητα μέτρου υ1 = 4 m/s, συγκρούεται κεντρικά και ελαστικά με άλλη ίδιου μεγέθους σφαίρα Σ2 που είναι δεμένη σε σχοινί μήκους ℓ του οποίου το άλλο άκρο είναι δεμένο ακλόνητα στην οροφή. Η Σ2 μόλις που δεν ακουμπά στο επίπεδο που κινείται η Σ1 και μετά την κρούση ανυψώνεται σε μέγιστο ύψος h1 = ℓ. Η σφαίρα Σ1 μπορεί να κινείται χωρίς τριβές στο οριζόντιο επίπεδο και κατά την κρούση της με τη Σ2, υφίσταται τη μέγιστη απώλεια στην κινητική της ενέργεια. Επαναλαμβάνουμε την διαδικασία αλλά αυτή τη φορά η Σ1 συγκρούεται πλάγια και ελαστικά με την Σ2 και μετά την κρούση η Σ2 ανυψώνεται σε ύψος h2 που είναι 64% μικρότερο από το h1. Να ... Διαβάστε περισσότερα |
|
|
|
|
|
|
|
Ένα σώμα Σ, μάζας m = 0,4 kg, ισορροπεί δεμένο σε νήμα με το άλλο άκρο αυτού δεμένο σε ακλόνητο σημείο Ο. Το σώμα με το νήμα μπορεί να περιστρέφεται χω ... Διαβάστε περισσότερα |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Σε ένα κύλινδρο μάζας Μ και ακτίνας R , ασκούμε μεσω κατάλληλου μηχανισμού μία σταθερή δύν&alpha ... Διαβάστε περισσότερα |
|
|
|
Ένα σώμα Σ1 είναι δεμένο στο κάτω άκρο κατακόρυφου ελατηρίου σταθεράς k. Ανεβάζουμε το σώμα μέχρι κάποια θέση και την χρονική στιγμή t0< ... Διαβάστε περισσότερα |
|
|
|
|
|
Στα παρακάτω σχήματα που περιέχουν πηγή (ιδανική ή μη) δύο λαμπάκια Λ1 και Λ2 (με αντιστάσεις R1 και R2) που θεωρούμε ότι συμπεριφέρονται σαν ωμικοί αντιστάτες θέλουμε να βρούμε τι θα συμβεί ως προς την φωτοβολία του Λ1 αν καεί το Λ2. Η φωτοβολία είναι ανάλογη με το ρεύμα που διαρρέει κάθε λαμπάκι και στην περίπτωση που αυξάνεται το ρεύμα η αύξηση είναι τέτοια ώστε να μην καεί το άλλο λαμπάκι.
Views:
1679
|
|
Date:
2017-05-11
|
|
|
|
|
|
Αρχικά ο &delt ... Διαβάστε περισσότερα |
|
|
|
|
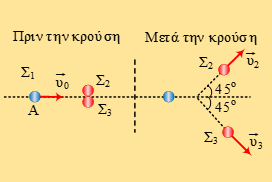 Τρεις λείες σφαίρες Σ1, Σ2 και Σ3, μάζας
Τρεις λείες σφαίρες Σ1, Σ2 και Σ3, μάζας 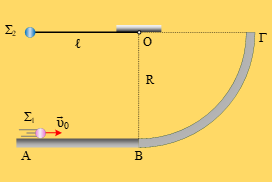 Σώμα Σ1 μάζας
Σώμα Σ1 μάζας 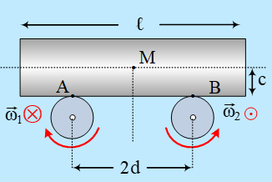 Μία ομογενής σανίδα με μάζα
Μία ομογενής σανίδα με μάζα 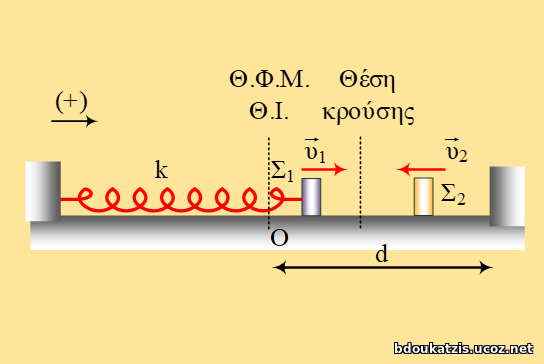
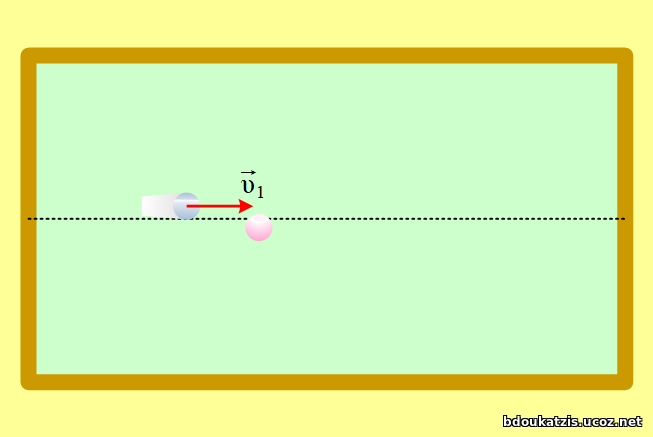
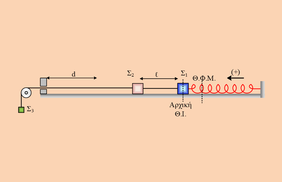 Στην διπλανή εικόνα βλέπουμε τα σώματα Σ1, με μάζα
Στην διπλανή εικόνα βλέπουμε τα σώματα Σ1, με μάζα 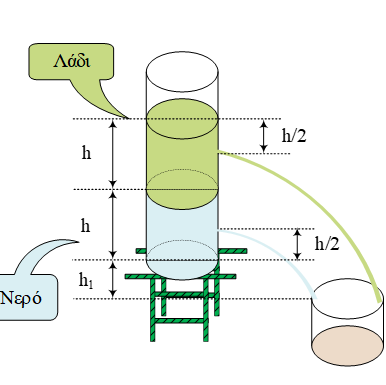 Κυλινδρικό δοχείο μεγάλου εμβαδού βάσης (
Κυλινδρικό δοχείο μεγάλου εμβαδού βάσης (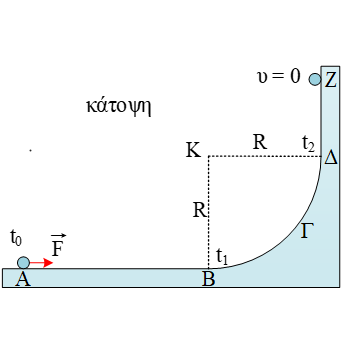 Σώμα μάζας
Σώμα μάζας 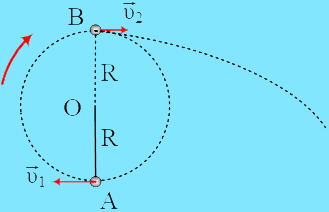
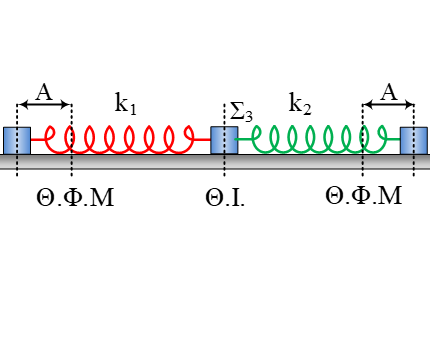 Δύο σώματα ίσης μάζας Σ1 και Σ2 βρίσκονται εκατέρωθεν σώματος Σ3 το οποίο παρουσιάζει με το δάπεδο τριβή, με συντελεστή με συντελεστή ορια&
Δύο σώματα ίσης μάζας Σ1 και Σ2 βρίσκονται εκατέρωθεν σώματος Σ3 το οποίο παρουσιάζει με το δάπεδο τριβή, με συντελεστή με συντελεστή ορια&
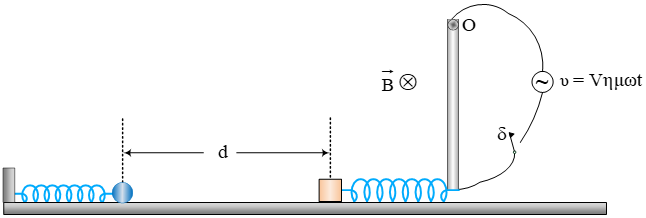 Ένα σώμα μάζας
Ένα σώμα μάζας 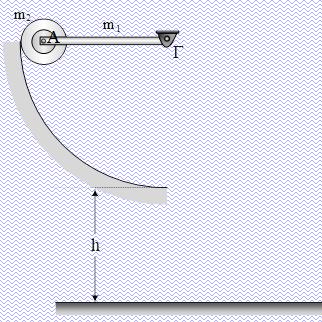 Στο σχήμα βλέπουμε μία ράβδο μάζας
Στο σχήμα βλέπουμε μία ράβδο μάζας 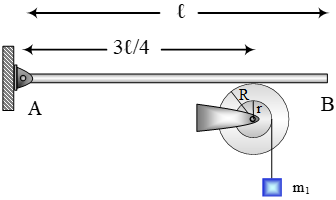 Κατασκευάζουμε ένα τροχό ενώνοντας τις βάσεις δύο ομογενών κυλίνδρων, έτσι ώστε να αποκτήσουν κοινό άξονα όπως δείχνει το σχήμα. Ο μεγάλος κύλινδρο&sigmaf
Κατασκευάζουμε ένα τροχό ενώνοντας τις βάσεις δύο ομογενών κυλίνδρων, έτσι ώστε να αποκτήσουν κοινό άξονα όπως δείχνει το σχήμα. Ο μεγάλος κύλινδρο&sigmaf
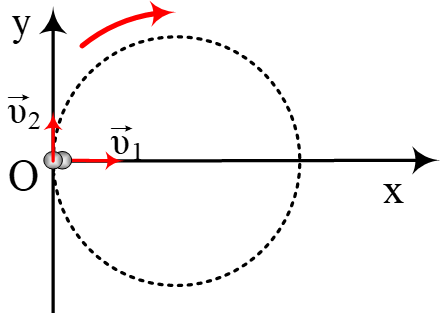 Από ένα σημείο Ο που το θεωρούμε ως αρχή των αξόνων, ξεκινάνε την χρονική στιγμή
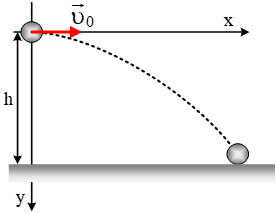
Από ένα σημείο Ο που το θεωρούμε ως αρχή των αξόνων, ξεκινάνε την χρονική στιγμή 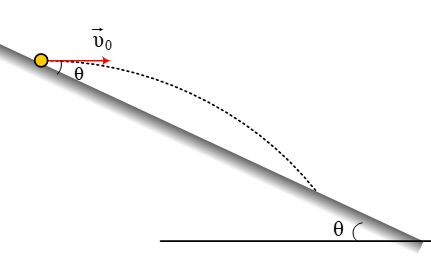 Από κάποιο σημείο κεκλιμένου επιπέδου εκτοξεύουμε σώμα, με οριζόντια ταχύτητα υ0, έτσι ώστε να προσγειωθεί σε κάποιο σημείο του κεκλιμένου επι&pi
Από κάποιο σημείο κεκλιμένου επιπέδου εκτοξεύουμε σώμα, με οριζόντια ταχύτητα υ0, έτσι ώστε να προσγειωθεί σε κάποιο σημείο του κεκλιμένου επι&pi
 Σώμα Σ μάζας
Σώμα Σ μάζας 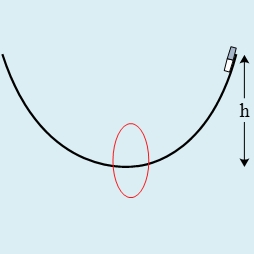 Στην διπλανή διάταξη ο μαγνήτης μάζας
Στην διπλανή διάταξη ο μαγνήτης μάζας 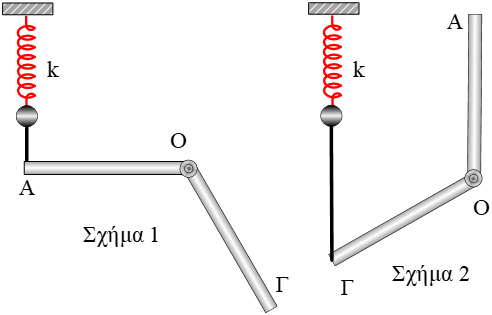 Στο διπλανό σχήμα βλέπουμε ένα κατακόρυφο ελατήριο σταθεράς
Στο διπλανό σχήμα βλέπουμε ένα κατακόρυφο ελατήριο σταθεράς 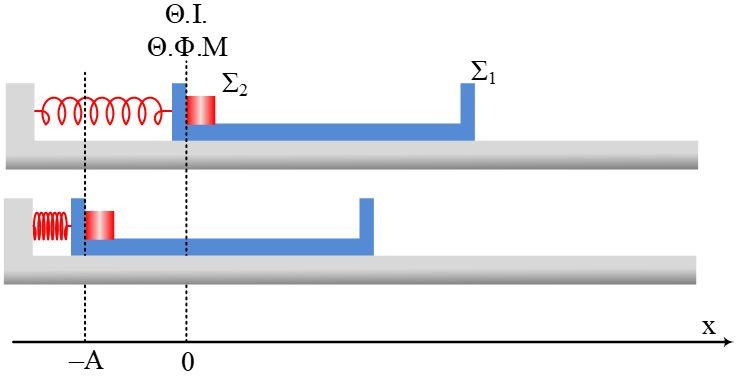 Στην διάταξη που φαίνεται στο σχήμα η πλατφόρμα Σ1, μήκους
Στην διάταξη που φαίνεται στο σχήμα η πλατφόρμα Σ1, μήκους 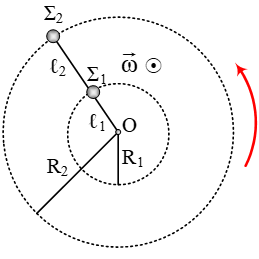 Τα σημειακά σώματα Σ1 και Σ2 που φαίνονται στην διπλανή εικόνα έχουν μάζες
Τα σημειακά σώματα Σ1 και Σ2 που φαίνονται στην διπλανή εικόνα έχουν μάζες 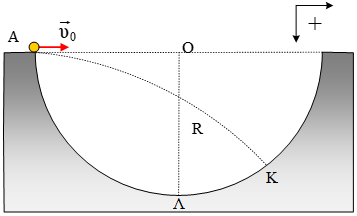 Από ένα σημείο Α(0, 0), του οριζοντίου επιπέδου εκτοξεύουμε μικρή σφαίρα Σ, μάζας
Από ένα σημείο Α(0, 0), του οριζοντίου επιπέδου εκτοξεύουμε μικρή σφαίρα Σ, μάζας 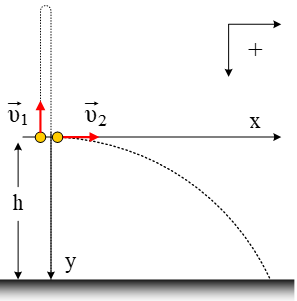 Δύο σώματα Σ1 και Σ2 μάζας
Δύο σώματα Σ1 και Σ2 μάζας 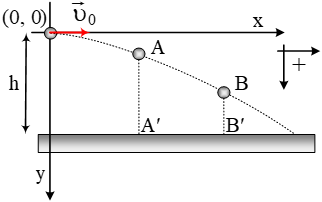 Σώμα μάζας
Σώμα μάζας 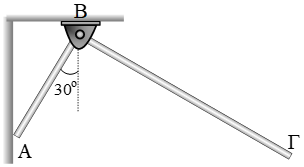 Δύο ράβδοι, η ΑΒ με μήκος ℓ και μάζα
Δύο ράβδοι, η ΑΒ με μήκος ℓ και μάζα 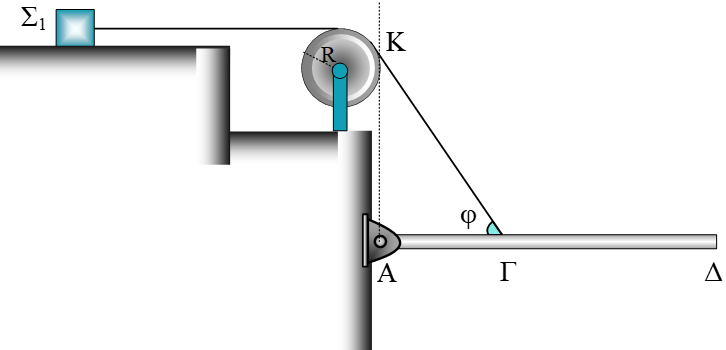 Στο διπλανό σχήμα βλέπουμε μία ράβδο μήκους ℓ = 2
Στο διπλανό σχήμα βλέπουμε μία ράβδο μήκους ℓ = 2 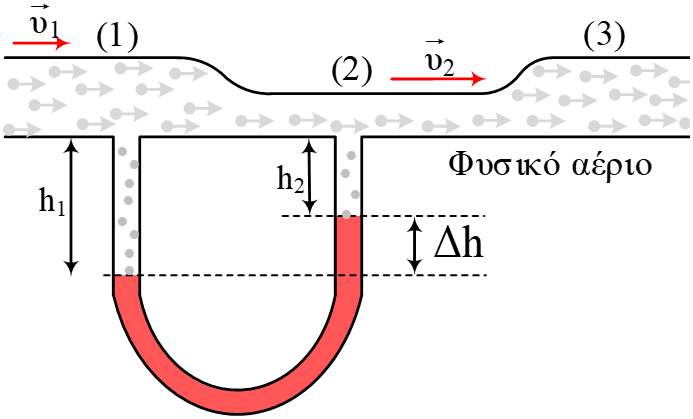 Στον
σωλήνα
Στον
σωλήνα 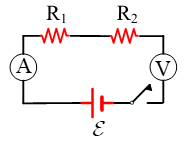 1.
1.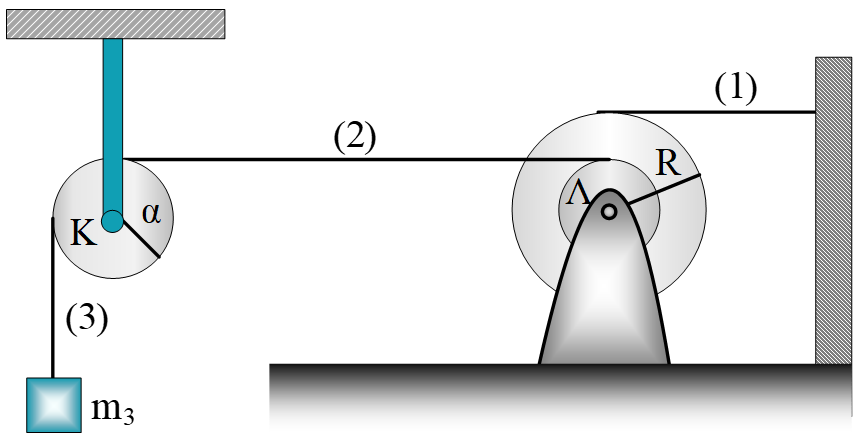 Μία διπλή τροχαλία μάζας
Μία διπλή τροχαλία μάζας 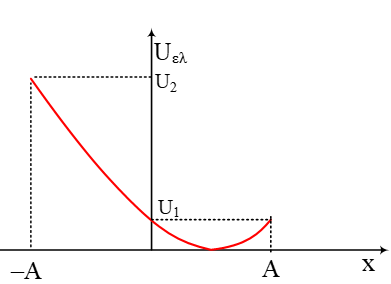 Ένα σώμα Σ μάζας
Ένα σώμα Σ μάζας 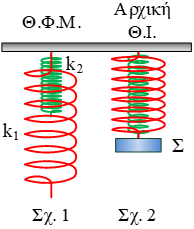 Στο διπλανό σχήμα βλέπουμε δύο ελατήρια (το ένα μέσα στο άλλο), όπου το εξωτερικό έχει σταθερά
Στο διπλανό σχήμα βλέπουμε δύο ελατήρια (το ένα μέσα στο άλλο), όπου το εξωτερικό έχει σταθερά 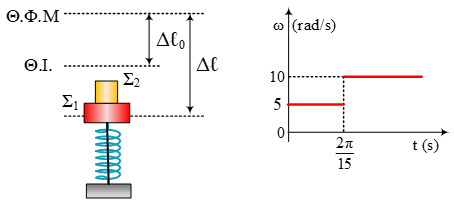 Ελατήριο σταθεράς
Ελατήριο σταθεράς 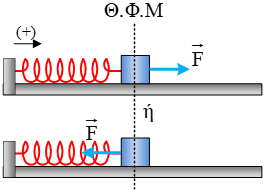 Σώμα μάζας
Σώμα μάζας 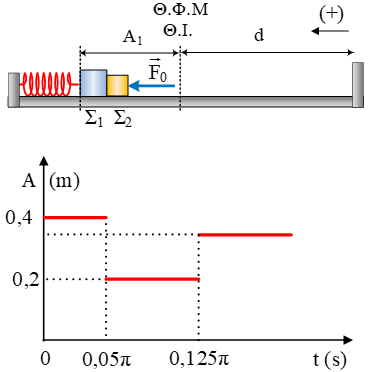 Στο διπλανό σχήμα βλέπουμε το οριζόντιο ελατήριο σταθεράς
Στο διπλανό σχήμα βλέπουμε το οριζόντιο ελατήριο σταθεράς 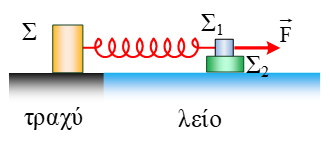 Στο διπλανό σχήμα βλέπουμε το σώμα Σ μάζας Μ = 10
Στο διπλανό σχήμα βλέπουμε το σώμα Σ μάζας Μ = 10 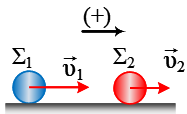 Δύο σφαίρες Σ1 και Σ2, με μάζες
Δύο σφαίρες Σ1 και Σ2, με μάζες 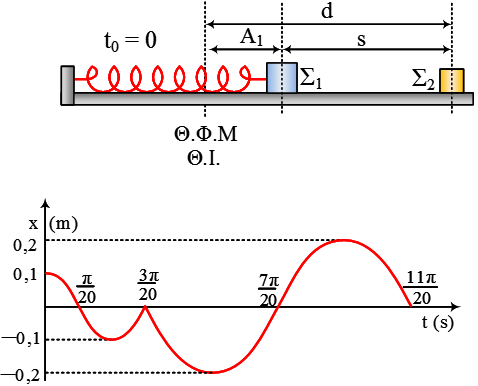 Στο διπλανό σχήμα βλέπουμε την εξέλιξη της ταλάντωσης ενός σώματος Σ1 μάζας
Στο διπλανό σχήμα βλέπουμε την εξέλιξη της ταλάντωσης ενός σώματος Σ1 μάζας 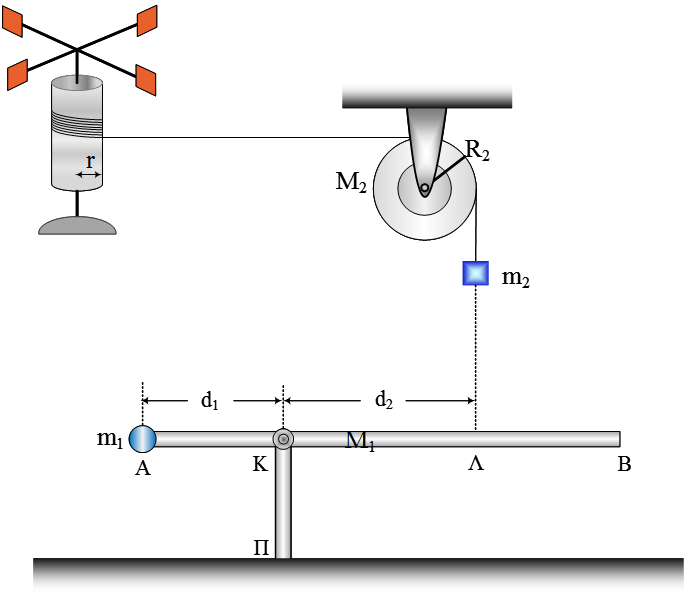 Ο κύλινδρος του σχήματος έχει ακτίνα
Ο κύλινδρος του σχήματος έχει ακτίνα 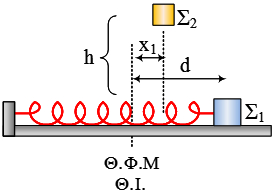 Ένα σώμα Σ1, μάζας
Ένα σώμα Σ1, μάζας 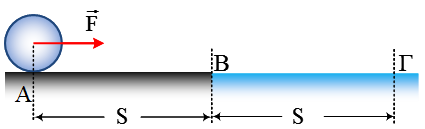
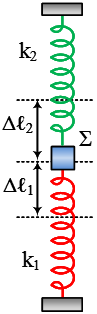 Στο διπλανό σχήμα τα δύο ελατήρια έχουν σταθερές
Στο διπλανό σχήμα τα δύο ελατήρια έχουν σταθερές 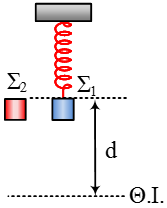
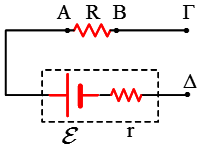 Στο διπλανό σχήμα βλέπουμε μία πηγή με εσωτερική αντίσταση
Στο διπλανό σχήμα βλέπουμε μία πηγή με εσωτερική αντίσταση 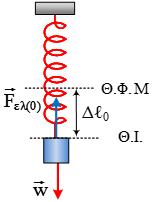 Ένα σώμα Σ μάζας m = 1
Ένα σώμα Σ μάζας m = 1 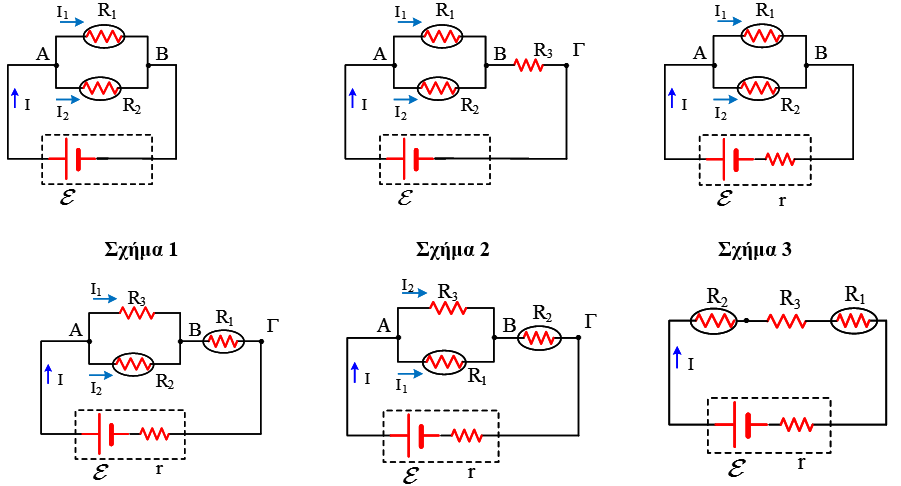
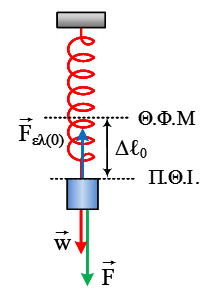 Ένα σώμα Σ μάζας m είναι δεμένο στο κάτω άκρο κατακόρυφου ελατηρίου σταθεράς
Ένα σώμα Σ μάζας m είναι δεμένο στο κάτω άκρο κατακόρυφου ελατηρίου σταθεράς 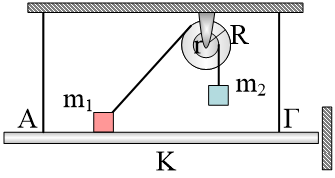 Στο διπλανό σχήμα η λεπτή ομογενής σανίδα έχει μήκος ℓ και μάζα
Στο διπλανό σχήμα η λεπτή ομογενής σανίδα έχει μήκος ℓ και μάζα 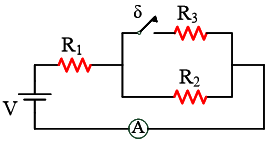 Το διπλανό κύκλωμα περιλαμβάνει μία πηγή συνεχούς τάσης, ιδανικό αμπερόμετρο και τους αντιστάτες
Το διπλανό κύκλωμα περιλαμβάνει μία πηγή συνεχούς τάσης, ιδανικό αμπερόμετρο και τους αντιστάτες 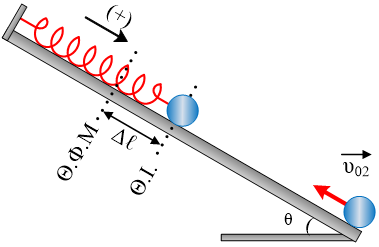 Στην κορυφή λείου κεκλιμένου επιπέδου (φ = 30ο) είναι στερεωμένο ιδανικό ελατήριο σταθεράς
Στην κορυφή λείου κεκλιμένου επιπέδου (φ = 30ο) είναι στερεωμένο ιδανικό ελατήριο σταθεράς 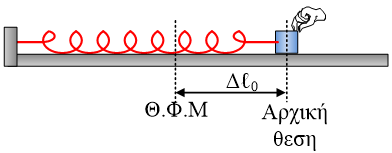 Το ελατήριο του σχήματος έχει σταθερά
Το ελατήριο του σχήματος έχει σταθερά