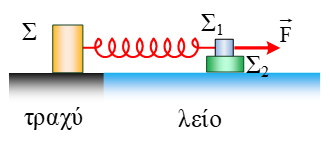
Στο διπλανό σχήμα βλέπουμε το σώμα Σ μάζας Μ = 10 kg, να βρίσκεται πάνω σε τραχύ δάπεδο με το οποίο παρουσιάζει συντελεστή τριβής μ₁ = 0,4. Το δεξιό του άκρο είναι συνδεδεμένο με ελατήριο σταθεράς k = 100 N/m, το άλλο άκρο του οποίου είναι δεμένο με σώμα Σ₁ μάζας m₁. Κάτω από το Σ₁, βρίσκεται το σώμα Σ₂ μάζας m₂ και παρουσιάζει με το Σ₁ τριβή με συντελεστή τριβής μ₂ = 1. Μεταξύ Σ₂ και δαπέδου δεν αναπτύσσεται τριβή. Αρχικά το ελατήριο έχει το φυσικό του μήκους και κάποια χρονική στιγμή ασκούμε στο Σ₁ σταθερή δύναμη F για μετατόπιση Δx. Μόλις το σύστημα των Σ₁ και Σ₂ σώμα αποκτήσει κατάλληλη ενέργεια ώστε κατά την διάρκεια της ταλάντωσης του να υπάρχουν στιγμές που μόλις που δεν μετακινείται το σώμα μάζας Μ. Η ταλάντωση των Σ₁, Σ₂ είναι της μορφής x = Αημ(10t + π/6) στο S.I. Η σταθερά του ιδανικού ελατηρίου είναι k = 100 N/m και στα σώματα Σ₁ και Σ₂ μόλις που δεν υπάρχει σχετική κίνηση μεταξύ τους σε κάποια σημεία της ταλάντωσής τους. Ως στιγμή t₀ = 0, λαμβάνουμε την στιγμή κατάργησης της δύναμης F. Να βρείτε:

α. την ενέργεια της ταλάντωσης του συστήματος

β. το μέτρο της δύναμης F

γ. τις σταθερές της ταλάντωσης D₁, D₂, των σωμάτων Σ₁, Σ₂.

δ. το μέτρο της στατικής τριβής που δέχεται το Σ₂ την στιγμή που η κινητική ενέργεια του ταλαντούμενου συστήματος αποτελεί το 25% της ενέργειας της ταλάντωσής του.

Δίνεται g = 10 m/s².