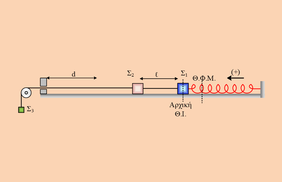
Στην διπλανή εικόνα βλέπουμε τα σώματα Σ₁, με μάζα m₁ = 1 kg και Σ₂, με μάζα m₂ = 3 kg που ισορροπούν στο λείο οριζόντιο επίπεδο με την βοήθεια ενός τρίτου σώματος Σ₃ μάζας m₃ = 0,5 kg όπως φαίνεται στην διπλανή εικόνα. Το ελατήριο είναι ιδανικό με σταθερά k = 100 N/m. Κάποια στιγμή ασκούμε στο σώμα Σ₂ οριζόντια δύναμη F με φορά προς τα αριστερά και με μέτρο που δίνεται από την σχέση F = 100x + 165 (S.I.) όπου xη απομάκρυνση από την αρχική θέση ισορροπίας του Σ₂. Ταυτόχρονα με την άσκηση της δύναμης F κόβουμε το νήμα που συνδέει το Σ₂ με το Σ₃. Μετά από χρονικό διάστημα Δt = √3 / 20   από την στιγμή που άρχισε να ενεργεί η δύναμη F την καταργούμε και ταυτόχρονα κόβουμε και το άλλο νήμα, που συνδέει τα Σ₁ και Σ₂. Την στιγμή που καταργούμε την δύναμη F (και που ταυτόχρονα κόβουμε το νήμα) το Σ₂ απέχει από τον αριστερό τοίχο απόσταση d = 0,15√3π m. Η κρούση του Σ₂ με τον τοίχο είναι ελαστική και στον γυρισμό του συγκρούεται πλαστικά με το Σ₁ την στιγμή που έχει ολοκληρώσει μία πλήρη ταλάντωση από την στιγμή που έμεινε μόνο του. Να βρείτε:

α. την ταχύτητα των Σ₁ και Σ₂ την στιγμή που κόβουμε το νήμα που τα συνδέει

β. το  πλάτος Α₁ της ταλάντωσης που εκτελεί το Σ₁ μετά την κατάργηση της δύναμης F

γ. το μήκος του νήματος ℓ που αρχικά συνδέει τα Σ₁ και Σ₂

δ. την απώλεια της μηχανικής ενέργειας κατά την κρούση των Σ₁ και Σ₂

ε. την δύναμη που ασκεί το Σ₁ στο Σ₂ όταν το ελατήριο είναι συσπειρωμένο και το συσσωμάτωμα κινείται με ταχύτητα μέτρου υ₁ = 1 m/s.

Η συνέχεια εδώ.