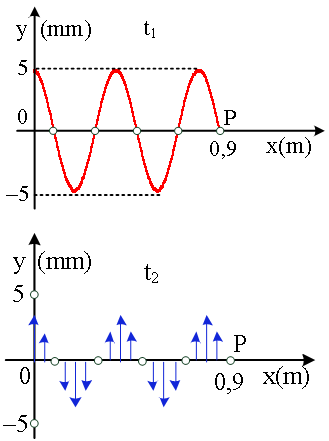
Σε γραμμικό ελαστικό μέσο διαδίδονται δύο κύματα με αντίθετες φορές, χωρίς απώλειες ενέργειας, οπότε και στο μέσο αυτό δημιουργείται στάσιμο κύμα. Μελετάμε μία περιοχή του χώρου, όπου στην θέση x = 0 θεωρούμε κάποια κοιλία του μέσου που ταλαντώνεται χωρίς αρχική φάση. Στα διπλανά σχήματα βλέπουμε δύο στιγμιότυπα του κύματος για την περιοχή που μελετάμε, τις χρονικές στιγμές t₁ όπου όλα τα σημεία του στάσιμου κύματος είναι ακίνητα και μία χρονική στιγμή t₂ = t₁ + 0,6 s, όπου όλα τα σημεία του ελαστικού μέσου έχουν απομάκρυνση από την θέση ισορροπίας y = 0. Για τις δύο χρονικές στιγμές ισχύει Δt = t₂ – t₁ < Τ, όπου Τ η περίοδος της ταλάντωσης των διαφόρων σημείων.

α. Να γράψετε την εξίσωση του στάσιμου κύματος

β. Να σχεδιάσετε το στιγμιότυπο του στάσιμου κύματος για τις θέσεις x_O = 0, έως x_Ρ = 0,9 m την χρονική στιγμή t₃ = 1,25 s.

γ. Να υπολογίσετε την διαφορά φάσης μεταξύ των σημείων Κ και Λ που βρίσκονται στις θέσεις x_K = 0,18 m και x_Λ = 0,58 m, αντίστοιχα καθώς και την διαφορά ΔΑ = Α_Κ – Α_Λ, όπου Α_Κ το πλάτος ταλάντωσης του σημείου Κ και Α_Λ το πλάτος ταλάντωσης του σημείου Λ.

δ. Κάποια στιγμή το σημείο Δ (x_Δ = 0,4 m) έχει ταχύτητα ταλάντωσης υ_Δ = 6π mm/s, ποια η ταχύτητα ταλάντωσης του σημείου Ζ (x_Z = 0,55 m) την ίδια χρονική στιγμή;

ε. Ποια η ελάχιστη αύξηση στην συχνότητα του κύματος ώστε το σημείο Ρ να ταλαντώνεται με μέγιστο πλάτος;