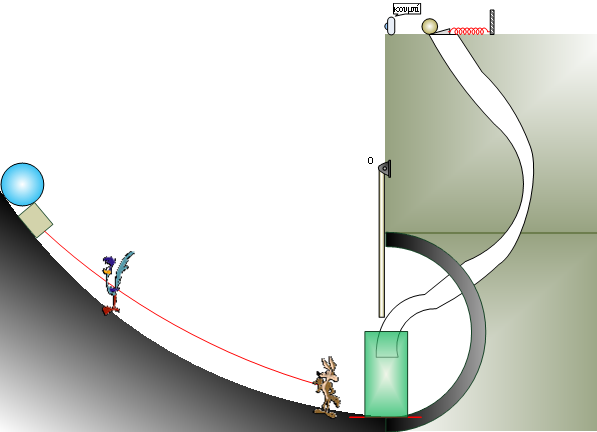
Το κογιότ θέλοντας να στήσει παγίδα στον Road Runner (= R.R.) τοποθετεί έναν βράχο σε μία πλαγιά ύψους Η = 6,25 m (το κέντρο μάζας του βράχου), από το κατώτερο σημείο της γειτονικής κοιλάδας που καταλήγει σε ημικύκλιο ακτίνας R = 2,5 m. Για να στηρίξει τον βράχο που έχει μάζα m = 70 kg και ακτίνα r = 0,5 m, τοποθετεί από κάτω έναν κύβο ακμής α έτσι ώστε ο βράχος μόλις που δεν τον υπερπηδά. Σε εκείνο το σημείο η καμπύλη πλαγιά έχει γωνία κλίσης θ = 60^ο. Το κογιότ μαζί με το αβαρές νήμα που έχει δέσει τον κύβο κάθεται στο κατώτερο σημείο της πλαγιάς και περιμένει τον R.R. να περάσει ώστε να τραβήξει το σχοινί να πατήσει ο βράχος τον R.R.. Κάποια στιγμή ο R.R. προσπερνά τον βράχο και κατευθύνεται προς το κρυμμένο κογιότ το οποίο τραβά το σχοινί. Βέβαια ο R.R. είναι πολύ γρήγορος και έτσι ο βράχος ισοπεδώνει το κογιότ. Στην συνέχεια ο βράχος συνεχίζει την πορεία του προς το ημικύκλιο και στο ανώτερο σημείο της τροχιάς του συγκρούεται με δοκό μήκους ℓ = 2,4 m και μάζας m₁ = 43,75 kg, που είναι αρθρωμένη σε σημείο Ο (στο πάνω άκρο της) γύρω από το οποίο μπορεί να στρέφεται χωρίς τριβές. Ο βράχος χτυπά την ράβδο σε απόσταση d από το σημείο Ο, με αποτέλεσμα αυτός να χάσει όλη την μεταφορική κινητική του ενέργεια ενώ η δοκός μόλις που φτάνει στο ανώτερο σημείο και ακουμπά με μηδενική (σχεδόν) ταχύτητα διακόπτη, (που είχε ξεμείνει εκεί από παλιότερη παγίδα του κογιότ), με αποτέλεσμα να ελευθερωθεί μία μικρή μπάλα κανονιού μάζας m₂ = 4 kg (αμελητέων διαστάσεων). Ο βράχος πέφτει κατακόρυφα και πετυχαίνει το κογιότ που μόλις είχε συνέλθει από το προηγούμενο χτύπημα. Η μπάλα αυτή ακολουθεί ένα χιονισμένο και παγωμένο μονοπάτι όπου ολισθαίνει χωρίς τριβές (και περιστροφές) που οδηγεί σε μία πόρτα ύψους h = 2 m και μάζας Μ = 12 kg η οποία μπορεί να στρέφεται γύρω από άξονα που περνά από το κατώτερο της σημείο (έδαφος) και ταυτίζεται με την κάτω της πλευρά. Η μπάλα κατά τις συγκρούσεις της με τα πλαϊνά τοιχώματα της διαδρομής της έχει χάσει ενέργεια Ε_απ. = 64 J. Η μπάλα πετυχαίνει την πόρτα σε σημείο που απέχειd₁ = 1,5 m από το έδαφος και μετά ακινητοποιείται (στιγμιαία). Να βρείτε: