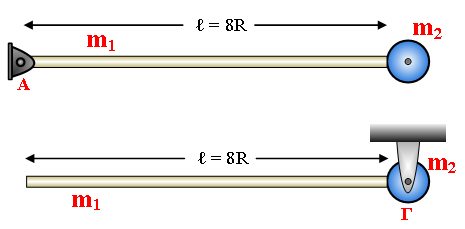
Μία ομογενής ράβδος μήκους ℓ = 8R και μάζαςm₁, είναι συγκολλημένη με ομογενή δίσκο ακτίνας R και μάζας m₂. Τα δύο στερεά σώματα είναι συγκολλημένα (άκρο ράβδου και περιφέρεια δίσκου) έτσι ώστε ο άξονας της ράβδου να περνά από το κέντρο του δίσκου. Το στερεό μπορεί να περιστρέφεται γύρο από άξονα που περνά από το ελεύθερο άκρο της ράβδου και είναι κάθετος στο επίπεδο που ορίζουν αυτή και ο δίσκος ή γύρω από άξονα που είναι κάθετος στο επίπεδο του δίσκου και περνά από το κέντρο του. Οι ροπές αδράνειας ως προς Α και ως προς Γ είναι ίσες.

Α. Ποια η σχέση που συνδέει τις δύο μάζες;

α.m₁ = 5m₂                            β.m₁ = 9m₂                            γ.m₁ = 12m₂

Β. Ποια σχέση συνδέει τις σταθερές ροπές που πρέπει να ασκήσουμε σε κάθε περίπτωση στο στερεό ώστε στην κατακόρυφη θέση να ακινητοποιηθεί;

α. τ₁ = τ₂                                 β. τ₁ = 9τ₂                               γ. τ₁ = 14τ₂

Να αιτιολογήσετε τις απαντήσεις σας.