0:04 AM ΠΑΜΕ ΚΟΥΒΑ (ΧΩΡΙΣ ΝΑ ΠΑΙΞΟΥΜΕ ΣΤΟΙΧΗΜΑ) |
α. το μέτρο της ταχύτητας υ1 β. την κάθετη δύναμη που ασκεί το τεταρτοκύκλιο στο σώμα μάζας m λίγο πριν το εγκαταλείψει γ. την απώλεια της ενέργειας του σώματος μάζας m κατά την ολίσθηση του στο τεταρτοκύκλιο δ. αν ο κουβάς έχει απώλεια ενέργειας κατά την κίνηση του στο οριζόντιο δάπεδο ίση με αυτή του σώματος μάζας m στο τεταρτοκύκλιο να βρείτε την απόσταση D ε. την κινητική ενέργεια του κουβά την στιγμή που συναντά το σώμα μάζας m. Δίνεται g = 10 m/s2, η ακτίνα του τεταρτοκυκλίου R = 0,55 m και ότι η στιγμή εκτόξευσης του κουβά είναι η στιγμή που το σώμα μάζας m εγκαταλείπει το τεταρτοκύκλιο. |
|
|
| Total comments: 0 | |
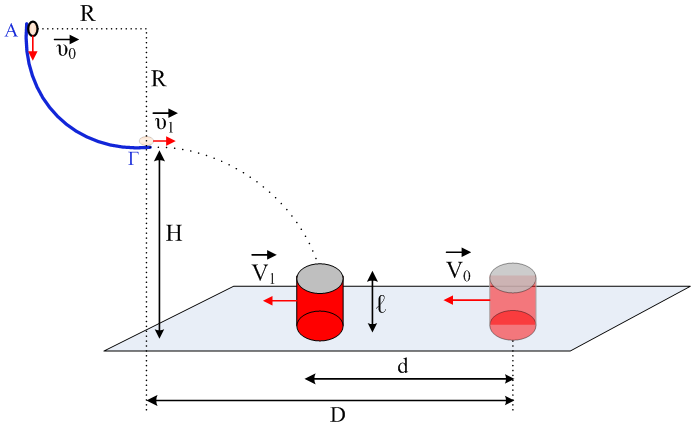 Σώμα μάζας
Σώμα μάζας 