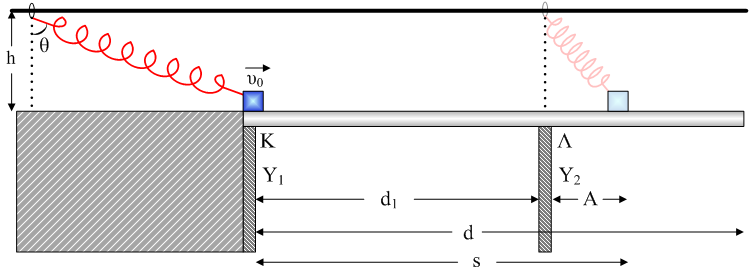
Ομογενής δοκός μήκους d = 2 m, και μάζας Μ, ισορροπεί οριζόντια πάνω σε κατακόρυφα υποστυλώματα που απέχουν μεταξύ τους απόσταση d₁ = 1,2 m, όπως φαίνεται στο διπλανό σχήμα. Πάνω από την δοκό και σε απόστασηh = 0,3 m υπάρχει τεντωμένο και αλύγιστο σύρμα, όπου μπορεί να κινείται με τριβή μικρός δακτύλιος αμελητέας μάζας. Στον δακτύλιο έχουμε δέσει το ένα άκρο ιδανικού ελατηρίου φυσικού μήκους ℓ₀ = 0,2 m και σταθεράς k = 100 N/m. Στο άλλο άκρο του ελατηρίου υπάρχει μικρό σώμα αμελητέων διαστάσεων και μάζαςm = 4 kg το οποίο μπορεί να κινείται χωρίς τριβές πάνω στην δοκό. Την στιγμή που το μικρό σώμα πατά πάνω στη δοκό ο άξονας του ελατηρίου σχηματίζει με την κατακόρυφο γωνία θ = 60^οκαι κινείται με ταχύτητα υ₀, ενώ όταν το σώμα διανύσει πάνω στην δοκό απόσταση s = 1,6 m, ακινητοποιείται και ο δακτύλιος εκείνη τη στιγμή βρίσκεται ακριβώς πάνω από το δεύτερο υποστύλωμα. Ο δακτύλιος μετά την ακινητοποίηση του δεν κινείται ξανά ενώ το μικρό σώμα εκτελεί ταλάντωση. Η δοκός κατά την διάρκεια της ταλάντωσης του σώματος μάζας m, μόλις που χάνει την επαφή με το υποστύλωμα Υ₁ όταν το μικρό σώμα δεν έχει κινητική ενέργεια.