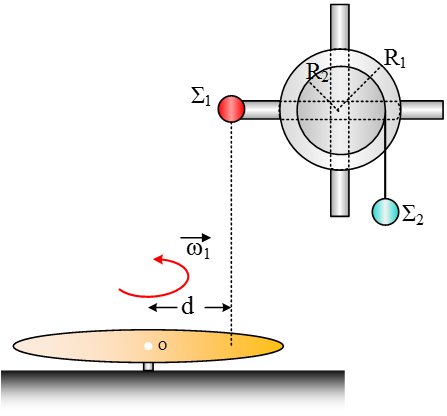
Στο διπλανό σχήμα βλέπουμε ένα στερεό που αποτελείται από έναν ομογενή κύλινδρο (I₁ = (1/2)M₁R₁² και δύο λεπτές ομογενείς ράβδους (I₂ = (1/12)M₂ℓ²) που είναι συγκολλημένες κάθετες μεταξύ τους και το κέντρο μάζας τους συμπίπτει με το κέντρο μάζας του κυλίνδρου, που βρίσκεται και ο άξονας που συγκρατεί το στερό. Σώμα Σ₁ μάζας m₁ αμελητέων διαστάσεων, βρίσκεται στο άκρο μιας ράβδου. Στον κύλινδρο έχουμε τυλίξει με σχοινί σώμα Σ₂ μάζας m₂ σε μία εγκοπή ακτίνας R₂. Κάποια στιγμή το σώμα Σ₁, αποκολλάται από την ράβδο και πέφτει πάνω σε δίσκο (Ι_δ = 0,9 kg·m²) που περιστρέφεται με γωνιακή ταχύτητα μέτρου ω₁ = 220 rad/s. Το σώμα Σ₁ με την κρούση του κολλάει πάνω στον δίσκο, σε απόσταση d = 0,3 m από το κέντρο του, με συνέπεια το σύστημα δίσκος Σ₂, να περιστρέφεται ως ένα ενιαίο σώμα με γωνιακή ταχύτητα μέτρου ω₂ = 200 rad/s. Στο σύστημα ράβδοι – κύλινδρος – Σ₂, μετά την αποκόλληση του Σ₁, η στροφορμή του μεταβάλλεται με σταθερό ρυθμό μέτρου (dL/dt)_συστ = 5 kg·m²/s² ως προς το κέντρο του κυλίνδρου. Τη στιγμή που το στερεό περιστρέφεται με γωνιακή ταχύτητα μέτρου ω = 10 rad/s, το σώμα Σ₂ έχει κινητική ενέργεια Κ₂ = 5 J. Να βρείτε: